Authors:
(1) Moritz Jasper, Barkhausen Institut gGmbH, Wurzburger Straße 46, Dresden, Germany ([email protected]);
(2) Stefan Kopsell, Barkhausen Institut gGmbH, Wurzburger Straße 46, Dresden, Germany ([email protected]).
Table of Links
Attacker Model and Security Goals
V. LCMSEC: THE PROPOSED PROTOCOL
This section describes the LCMsec protocol in detail. LCMSec employs a hybrid cryptographic system: Messages in transit are encrypted and authenticated using symmetric-key cryptography to achieve confidentiality, integrity and authenticity as outlined in Section IV. The symmetric key used to this end is generated by an authenticated group key agreement protocol that does not depend on any central instance to facilitate. We assume however that each participant possesses a digital identity with which he can express his rights to the system, details on this can be found in Section V-B1.
In the following, we first present our solution for securing the messages under the assumption that each participant already has knowledge of required keying material. The generation of this keying material is discussed subsequently.
A. Security of Messages in Transit
We maintain the hierarchy between channel and group that is inherent to LCM – one participant can be active on any number of multicast groups, and on any number of channels within that group. However, participants should only be able to read and send messages on the LCMDomains that they have permissions to use. Thus, to maintain confidentiality and
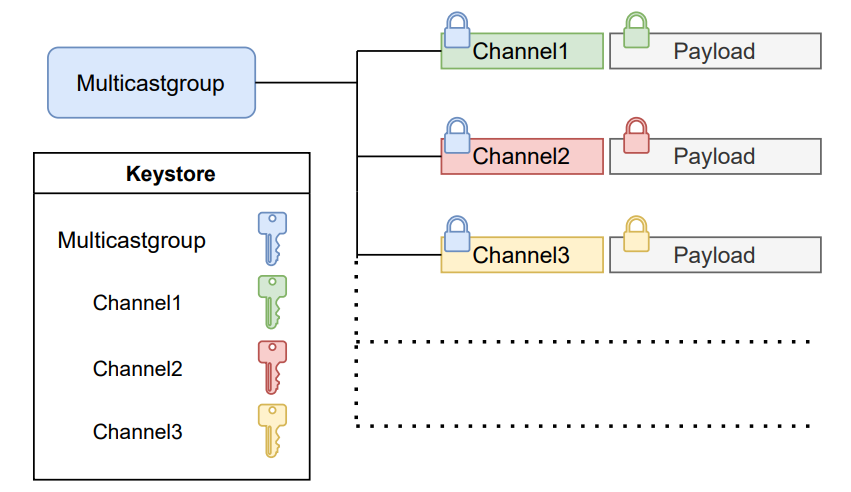
accountability on a per-channel level, we use a hierarchical scheme illustrated in Figure 3: one key, kg, is used to secure the channelname. This key is shared between all users with the permission to access the multicast group. A second key, kch, is used to secure the message itself — this key is shared by all users with permission to access the LCMDomain
A receiver can use kg to decrypt the channelname, then look up the associated kch to decrypt the message. This carries with it a concession in terms of confidentiality: If an attacker has access to kg (he might have access to another channel within that group), he can learn the channelname of messages on other channels. However, the alternative – encrypting the channelname and payload with a single key which is unique to the LCMDomain – would require a subscriber to attempt decryption of the message with every key that he knows for the group, until he succeeds. This clearly does not scale for many topics in one group.
1) Symmetric encryption of LCM messages: We ensure confidentiality and authenticity of LCMsec messages through the use of authenticated encryption. Specifically, we use AES in Galois/Counter Mode (GCM) in accordance with the NIST recommendations [19]. Using the GCM mode of operation requires specifying an Initialisation Vector (IV), which must be unique for each message encrypted with the same key

While a sequence number is already part of the LCM header, multiple parties might be communicating on one channel with the same key. Since they increment their sequence number separately, we also need to uniquely identify senders to form a unique IV. To this end, we use a 16-bit sender ID. According to the NIST recommendations, we construct a deterministic 96-bit IV as shown in Figure 4. The salt, which has not yet been discussed, will be generated as part of the keying material described in Section VI-B.
The LCMsec packet format shown in Figure 5 is similar to the LCM packet format. The fields are explained in the following:
magic : Number used to identify LCMsec protocol messages.
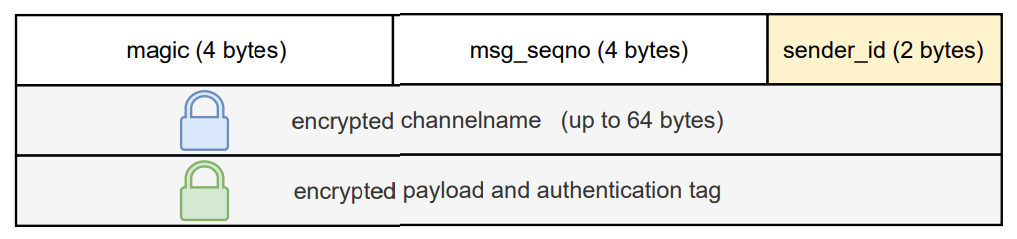
msg seqno : Message sequence number.
sender id : Unique identifier associated with the node sending the message. Its generation is covered in section V-B.
channelname : Zero-terminated and ASCII-encoded channelname, encrypted with kg and AES-CTR. A receiver can decrypt the channelnname bytewise until finding the nullterminator. Unauthenticated encryption is used for the channelname in order save the overhead of a separate authentication tag. Authentication of the channelname is instead guaranteed by including it in the authentication of the payload.
payload : The AES/GCM encrypted message including authentication tag, encrypted with kch. The channelname is included as associated data of the AES/GCM mode.
The spatial overhead of the scheme compared to LCM is thus 18 bytes: two for the sender id and 16 for the authentication tag produced by GCM.
- Fragmented messages: As explained in Section III, messages that do not fit into a single UDP packet are supported by LCM and called fragmented messages. In LCMsec, we encrypt and authenticate these messages before they are fragmented (and conversely decrypt and verify them after they are joined back together). This approach authenticates not only the content of the fragment, but also their order.
- Out-of-order messages and replay attacks: Since LCM employs UDP-multicast, messages might arrive out of order. However, with the introduction of sender IDs, the pair msgid = (sender_id, seqno) is a unique identifier for each message. Therefore, it now becomes feasible to detect and discard or even correct the order of out-of-order messages. Such behaviour may optionally be configured in LCMsec.
More importantly, the msgid functions to prevent replay attacks. To keep track of already received messages, a sliding window of the greatest sequence number received for each peer can be used, in addition to a window of previously received messages. To efficiently keep track of this window, the algorithm in appendix C of RFC2401 [20] or RFC6479 [21] can be used.
B. Group Discovery and Key Agreement
This section describe how the shared symmetric keying material is generated. Sharing a key with other users is only meaningful if a notion of identity and associated permissions exists – specifically, the permission to send or receive on the LCMDomain. The scheme used to this end is described in Section V-B1.
Subsequently, we will describe the protocol used to perform the key agreement on the group. We use the Dutta Barua group key agreement [17] to generate a key among participants, but this does not suffice: it is simply the backing algorithm used to perform the key agreement. Thus, the key agreement process is split into two phases. The first one is a setup phase, which aims to achieve consensus within the group on the parameters used to perform the DBGKA – we will call this phase group discovery, described in Section V-B3. The second one is the DBGKA itself which establishes the shared group key, to be described in Section V-B2.
Here, we only discuss the key agreement protocol for a single LCMDomain. In the case of multiple channels, multiple runs of this protocol will be performed. Indeed, most of the time, at least two runs of the key agreement protocol will be performed simultaneously: one to generate kg, another one to generate kch.
1) Certificate and permission management: Certificate and permission management is not the main focus of this work, and the solution presented here can easily be changed or extended: it is not tightly coupled to the other areas of this work. Nevertheless, we present an attribute-based access control mechanism based on X.509 certificates [22] that is used to both identify participants and manage their permissions.
A user U has access to a specific LCMDomain L if it possesses a valid X.509 certificate which includes an identifier IDU that uniquely identifies it on the LCMDomain L. This IDU , which is understood to be the identity for that user on L is encoded into the URN of the Subject Alternative Name Extension (SAN) of the certificate in accordance with RFC 5280 [22]. A Certificate Authority (CA) can issue this certificate and generate the unique identifier for each domain by incrementing it. The SAN’s used shall be of the form
urn: lcmsec: <group> : <channel> : <id>
Multiple SANs can be present in one certificate, enabling an entity to be active on multiple LCMDomains.
2) Dutta Barua key agreement: To agree on a key among entities of an LCMDomain, the Dutta Barua authenticated group key agreement (DBGKA) is used [17] [1]. The protocol is Diffie-Hellman based and has a number of properties that are interesting for our use-case. Namely, it is a two-round key-agreement algorithm that uses broadcast in the second round, which fits the communication topology used in LCM. Additionally, it is a dynamic protocol: Entities can join a group of users that have already agreed upon a key amongst themselves while taking advantage of previously computed values, greatly increasing scalability by reducing both the number of network transmissions and computations that need to be performed.
The DBGKA provides three operations:
KeyAgree() : It allows a number of users to agree on a shared key
Join() : If a set of users (participants) P has already performed a KeyAgree() operation, this operation provides a way for another set of users (joining users), J, to agree on a shared symmetric key among P ∪J. This operation is far more efficient than performing KeyAgree(P ∪ J) in terms of network usage: in addition to J, only 3 users within P need to be active on the network.
Leave() : Users can leave group, which causes a new key to be generated among the remaining users.
However, to use the DBGKA in practice, we need an additional phase which serves to (1) discover peers and arranges them in a circle, (2) exchange the certificates of each participant and (3) synchronise the start of the key agreement operations. In the brokerless spirit of LCM, we aim to achieve these prerequisites without a central instance to coordinate. We will call the protocol we use to achieve this the LCMsec group discovery protocol, to be presented in the following section.
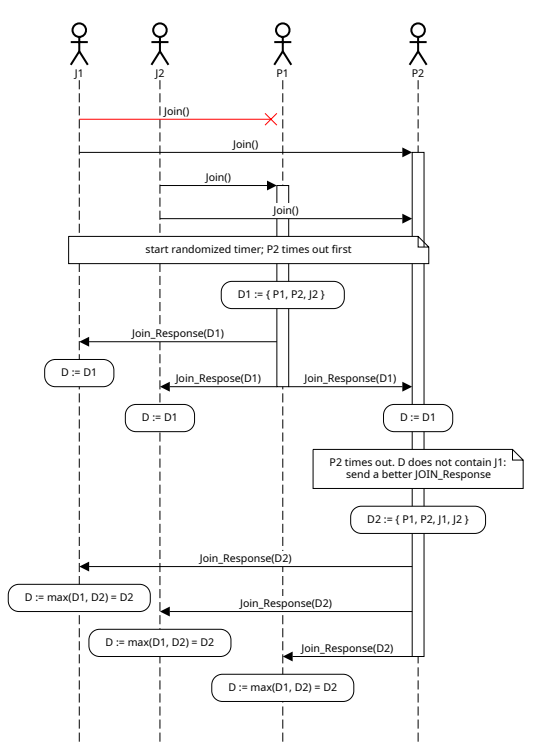
3) Group discovery: As discussed in Section V-B1, a group G of entities might have a certificate that grants them permission to be active on an LCMDomain. However, only a subset of these may be active at a specific point in time – e.g., certain devices may be turned off or disconnected from the system in an IoT context. Within G, we define two subsets: Firstly P denotes the set of entities that have already agreed upon a shared secret. Secondly, J consists of the entities that are connected to the network and have expressed their intention to join P.
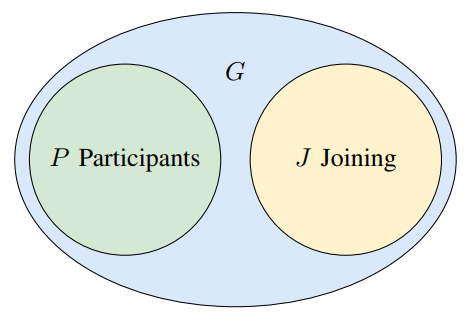
First, we note that for the purposes of the group discovery protocol, there is no need for a separate initial KeyAgree() and subsequent Join() operation: without loss of generality, P may be empty, and both cases can be handled by a Join() operation.
Additionally, we note that the problem of arranging participants in a circle is equivalent to achieving consensus on the sets of P and J among all U ∈ P ∪ J. They can then be ordered by their unique identifiers (IDU ). Alternatively, a hash of their certificate could be used. Subsequently, a deterministic mapping to sender IDs (that is, an unsigned integer which fits into 16 bits) can be performed. The synchronisation of the KeyAgree() operation can also be regarded as part of this consensus problem: the consensus on a timestamp t at which the key agreement shall commence.
The problem of consensus in distributed computing is wellstudied. A popular solution is the RAFT Protocol [18], which achieves consensus among a group of distributed nodes by voting for a leader via a randomised timeout, who then replicates a log data structure to all other nodes. In our group discovery protocol, we take the lessons learned from RAFT and adapt them to our use-case by noticing that replication of a log data structure is not what we desire: We do not care about consensus on data in the past, only the current sets P and J are of interest. Additionally, we do not require a strict form of consensus: The DBGKA will reliably fail if there is no consensus on the participants involved (instead of producing an invalid key). Finally, we notice that RAFT uses heartbeats to ensure that a leader always exists, which is problematic in a multicast communication topology due to scalability issues. However, a leader is not always needed, but only when a Join() operation is initiated.
e thus present the central idea of our group discovery protocol. Unlike RAFT, we form consensus only on an asneeded basis (that is, whenever a new key is necessary) and vote for a leader not via timeout, but instead form consensus on the data itself. By defining (P, J, t) ∈ D, we can impose a weak order on D: for D1 = (P1, J1, t1) and D2 = (P2, J2, t2), D1, D2 ∈ D,
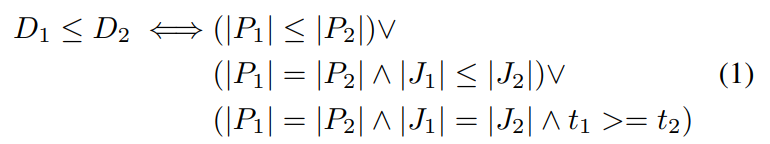
By adding a small, random offset ε to t, this weak order can be transformed into a total order. The way we define this order is not arbitrary: we maximise |J| and |P|, while minimising t to guarantee termination of the discovery phase. Consensus is now simply achieved by each participant keeping track of the largest D it has observed.

Once t has been reached, the DBGKA will be initiated and no further modification to D is permitted until it fails or succeeds. If successful, each participant will set P := P ∪ J and J := ∅, otherwise they will set P := ∅ and J := ∅ and restart the group discovery phase by transmitting a JOIN.
This paper is available on arxiv under CC BY 4.0 DEED license.
[1] Two attacks on the DBGKA protocol have been presented in [23]. We have analysed the attacks and conclude that they are not relevant for our solution. Details on this are given in Appendix A.

